Desde "Matemático Soriano", os deseo feliz Navidad a todos, pero claro, a mi manera matemática.
Arcos de San Juan de Duero

domingo, 25 de diciembre de 2016
sábado, 17 de diciembre de 2016
FÓRMULA DE HERÓN
Continuando con elementos que me gustaría explicar a los alumnos de las Becas Europa, me dispongo ahora a hablar sobre la fórmula de Herón.
 |
| Herón de Alejandría |
Cuando trabajamos en geometría, los triángulos son muy importantes, y si tenemos una forma de calcular el área del mismo utilizando solo los lados de este, puede resultarnos muy útil. Y esto es lo que conseguimos gracias a la fórmula de este matemático griego. La expresión de la misma sería la siguiente:
Un caso para el cual considero está fórmula muy práctica es cuando tenemos los vértices de un polígono convexo y conocemos sus coordenadas en un plano. Así, triangulando el polígono sobre uno de sus vértices podemos calcular el área de este solo con el valor de los lados y de las diagonales (lo podemos sacar a partir de los vértices), calculamos las áreas de los distintos triángulos con esta fórmula y luego las sumamos. En la siguiente figura vemos un ejemplo de lo propuesto, triangulamos sobre el vértice superior y con las diagonales y los lados calculamos el área de cada triángulo, al sumarlas todas obtendremos el área total.
 |
| Ejemplo de la triangulación propuesta |
GRAFO DE VORONOI
Esta entrada va dirigida en especial a los alumnos que están participando ahora mismo en la cuarta fase del Programa de Becas Europa y que al leer el pequeño ensayo resumen que he compartido hayan sentido curiosidad por saber que es el grafo de Voronoi y sobre cómo funciona, cómo se usa y para qué se utiliza. A los que no os encontréis en está situación os invito también a leer esta pequeña descripción del grafo Voronoi y a participar en las Becas Europa, como experiencia personal, puedo decir que es un programa que me está resultando bastante interesante y que recomendaría a cualquiera. Sin entretenerme más voy a comenzar con la explicación de este curioso y útil grafo:
En primer lugar, el grafo de Voronoi es aquel que permite hallar las "zonas de influencia" de un punto en el plano. Y ahora, ¿a qué diantres le estoy llamando "zona de influencia"? Una "zona de influencia" de un punto P es aquella región del plano para la cual el punto que se encuentra a una menor distancia de todos los puntos que componen esta región será P. Por ejemplo, si tenemos dos puntos A y B, la "zona de influencia" de estos quedará definida por la mediatriz entre ambos, como vemos en la siguiente figura, donde la zona de A será la azul y la de B la naranja:
Este es un ejemplo muy claro, pero, ¿qué pasaría si tengo más de dos punto?, por ejemplo, 3. En este caso, tendría que dibujar las mediatrices dos a dos y de forma cuidadosa elegir los puntos de corte que delimitarán mis "zonas de influencia". A continuación se muestra en la siguiente imagen, la zona de influencia de A será la azul, la de B la naranja y la de C la amarilla.
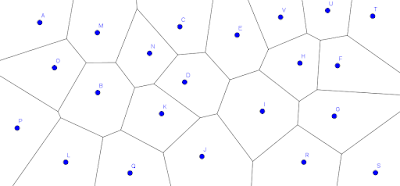
El proceso resultaría similar con más puntos, realizamos las mediatrices entre puntos cercanos y tras ello, decidimos de forma intuitiva cuales serán los vértices (puntos de corte de mediatrices) de nuestras "zonas de influencia". Aquí podéis ver un ejemplo con varios puntos y su grafo de Voronoi asociado.
Este grafo se ha utilizado en múltiples ocasiones desde que fuera inventado por el ruso Gueorgui Voronói. En temas tan diversos como estudios sobre la rentabilidad de un posible nuevo establecimiento comercial (se estudiaría cuál sería la "zona de influencia" del local) hasta la planificación de estrategias militares, como cuando los japoneses atacaron a Estados Unidos en la batalla de Pearl Harbor durante la Segunda Guerra Mundial. Ellos afirman que dibujaron un grafo de Voronoi poniendo como puntos las bases estadounidenses del Pacífico, entonces, al hacer volar a sus aviones por las líneas del grafo (los lugares más alejados de los puntos en el grafo) lograron esquivar los detectores del enemigo y presentarse por sorpresa. Ahora, en el proyecto emprendido en Becas Europa, pretendo dibujar el grafo que sea más adecuado para las necesidades de los refugiados y a partir de él, extraer los puntos que cumplen dicho grafo (el proyecto de Becas Europa sobre el que hablo se relaciona en aportar algo que pueda ayudar a la construcción de un nuevo campo de refugiados de 50.000 personas que va a construirse próximamente en Europa y, cómo no, yo he considerado que aquello con lo que más ayuda podía ofrecer era utilizando las matemáticas, la herramienta que mejor domino y con la que más disfruto trabajando).
Espero que os haya gustado esta pequeña explicación del grafo de Voronoi y que aquellos que estáis participando conmigo en Becas Europa os haya resultado una herramienta interesante y que hayáis entendido mejor que es lo que quiero hacer en mi proyecto y como funciona este grafo.
martes, 13 de diciembre de 2016
TANGRAM, 100 FIGURAS EN 1 MINUTO
Aquí os dejo con un vídeo titulado "Tangram 100 figuras en 1 minuto" para que podáis iniciaros o adquirir nuevas ideas en este genial puzle.
sábado, 26 de noviembre de 2016
PAUL DIRAC INTRODUCCIÓN DE SU VIDA
Dado el éxito que tuvo la semana pasada el vídeo de Paul Dirac, he decidido colgar la primera parte también. En ella se explica un poco, cómo fue la vida de este hombre. Espero que os guste.
miércoles, 23 de noviembre de 2016
PAUL DIRAC Y LA ANTIMATERIA
En este os dejo con un clarísimo ejemplo de lo que es una "idea feliz" en matemáticas. En este vídeo se explica la deducción teórica de la antimateria, antes incluso de que se hubiera deducido experimentalmente (de forma excelente dicho sea de paso, a mí me encantó el vídeo la primera que lo vi).
viernes, 11 de noviembre de 2016
SI FERMAT HUBIESE SIDO COMPOSITOR
Si Fermat hubiese sido compositor...

"Canon en D"
Tengo una canción realmente pegadiza, pero este margen es demasiado pequeño.

"Canon en D"
Tengo una canción realmente pegadiza, pero este margen es demasiado pequeño.
viernes, 28 de octubre de 2016
domingo, 16 de octubre de 2016
sábado, 15 de octubre de 2016
viernes, 14 de octubre de 2016
INTERIOR DE UN TORO
En matemáticas, un toro es una figura topológica caracterizada por tener un agujero, es decir, que podría hacerse un nudo con una cuerda sin que se soltará o mejor dicho escurriera (como pasaría en una esfera).


jueves, 13 de octubre de 2016
miércoles, 12 de octubre de 2016
martes, 11 de octubre de 2016
lunes, 10 de octubre de 2016
LA SEMANA DE LA ILUSIÓN ÓPTICA
Desde hoy y hasta el domingo vamos a poner en este blog, una entrada dedicada a las ilusiones ópticas, a lo que parece pero que en realidad no es, a lo que hay detrás de las apariencias, a retar a los sentidos. Y, ¿cómo no?, para empezar la semana os dejo con uno de los dibujos más famosos del artista que era capaz de engañar a los sentidos, Escher. Espero que disfrutéis con las ilusiones de esta segunda semana de octubre.

viernes, 30 de septiembre de 2016
ACERTIJO 60 - DETRÁS DE LA INECUACIÓN III
Llegamos al final de este segundo mes de acertijos con este problemilla "extremo" (de ahí que los dos anteriores fueran similares, para preparar este). Espero que os haya gustado mucho estos retos diarios y que disfrutéis con este último desafío (uno de los más complicados de la historia del blog).
Sea n ≥ 2 un número entero. Determinar el menor número real positivo γ de modo que para cualesquiera números reales positivos x1, x2,... ,xn y cualesquiera números reales y1, y2,... ,yn con 0 ≤ y1, y2,...,yn ≤ 1/2 que cumplan x1 + x2 + ... + xn = y1 + y2 + ... + yn = 1, se tiene que
x1x2 ...xn ≤ γ (x1y1 + x2y2 + ... + xnyn)
La solución se muestra más abajo
jueves, 29 de septiembre de 2016
ACERTIJO 59 - DETRÁS DE LA INECUACIÓN II
Si a y b son dos números reales diferentes, resolver el sistema:
x + y = 1
(ax + by)^4 =< a^4 *x + b^4 *y
* =< significa menor o igual.
La solución se muestra más abajo.
miércoles, 28 de septiembre de 2016
ACERTIJO 58 - DETRÁS DE LA INECUACIÓN
Si a y b son dos números reales diferentes, resolver el sistema:
x + y = 1
(ax + by)^2 =< a^2 *x + b^2 *y
* =< significa menor o igual.
La solución se muestra más abajo.
martes, 27 de septiembre de 2016
ACERTIJO 57 - INYECCIONES CURIOSAS
A cada entero positivo n se le asigna un entero no negativo f(n) de tal manera que se satisfagan las siguientes condiciones:
f(r*s) = f(r) + f(s)
f(n) = 0, siempre que la cifra en las unidades de n sea 3
f(10) = 0
Hallar f(1985). Justificar la respuesta.
La solución se encuentra más abajo.
f(r*s) = f(r) + f(s)
f(n) = 0, siempre que la cifra en las unidades de n sea 3
f(10) = 0
Hallar f(1985). Justificar la respuesta.
La solución se encuentra más abajo.
lunes, 26 de septiembre de 2016
ACERTIJO 56 - EN BUSCA DE LAS TERNAS
Hallar todas las ternas de enteros (a,b,c) tales que:
a+b+c=24
a^2+b^2+c^2=210
a*b*c=440
La solución se encuentra más abajo.
a+b+c=24
a^2+b^2+c^2=210
a*b*c=440
La solución se encuentra más abajo.
domingo, 25 de septiembre de 2016
ACERTIJO 55 - EL ACERTIJO DEL 7
Calcula la suma S de los n sumandos:
S = 7 + 77 + 777 +...+ 7...7
La solución se muestra más abajo.
S = 7 + 77 + 777 +...+ 7...7
La solución se muestra más abajo.
sábado, 24 de septiembre de 2016
ACERTIJO 54 - UNO DE ÁNGULOS
En un triángulo ABC tenemos puntos D y E respectivamente de AB y AC. Conocemos la medida de los ángulos indicados a continuación: ABE=30º, EBC=50º, ACD=20º y DCB=60º. Hallar el valor del ángulo EDC.
La solución se muestra más abajo.
La solución se muestra más abajo.
viernes, 23 de septiembre de 2016
ACERTIJO 53 - LAS 5 CIFRAS FINALES DEL CUADRADO
Halla un número de 5 cifras tal que su cuadrado termine en las mismas 5 cifras colocadas en el mismo orden.
La solución se encuentra más abajo.
La solución se encuentra más abajo.
jueves, 22 de septiembre de 2016
ACERTIJO 52 - EL PUZZLE DE LA CRUZ GRIEGA Y EL CUADRADO
Corta una cruz griega (aquella cuyos lados son todos iguales) en cuatro partes de tal forma que puedas volverlos a juntar formando un cuadrado. Intenta hacerlo de tal forma que las cuatro piezas sean iguales.

La solución se muestra en el enlace.

La solución se muestra en el enlace.
miércoles, 21 de septiembre de 2016
ACERTIJO 51 - TABLAS 3x3 Y 5x5
¿Para qué valores de n entero, 0 < n < 9, es posible marcar algunas casillas en una tabla 5x5 de manera que cada cuadrado 3x3 en ella contenga exactamente n casillas marcadas?
La solución se muestra tras el enlace.
martes, 20 de septiembre de 2016
ACERTIJO 50 - EL CONO Y LA ESFERA
Una esfera de radio 15 se mete en un cono, cuya generatriz es igual al diámetro de la base, como se muestra en la figura. ¿Cuál es la altura del cono?
La solución se muestra tras el enlace.
lunes, 19 de septiembre de 2016
ACERTIJO 49 - LA FLOR INSCRITA EN EL CUADRADO
En la figura ABCD es un cuadrado de lado 1 y los cuartos de círculo tienen centros en A, B, C y D.. ¿Cuál es la longitud de PQ?
La solución se muestra tras el enlace.
domingo, 18 de septiembre de 2016
ACERTIJO 48 - EL PAGO AL REY II
El rey de un país oriental tiene un gobernador en cada una de sus provincias que anualmente llevan su tributo, consiste en un saco con un número indeterminado de monedas de oro de p gramos. Varios de los gobernadores hace trampa: todas sus monedas pesan un gramo de menos sin variar forma y tamaño (tienen una burbuja de aire en su interior). Con una balanza de dos platillos y un juego de pesas apto para pesar cualquier cantidad el rey tiene que averiguar en ¡una única pesada! cual es el gobernador que pretende engañarle. No es necesario saber cuántos gobernadores hay ni cuál es el tributo que paga cada uno.
La solución está tras el enlace.
sábado, 17 de septiembre de 2016
ACERTIJO 47 - EL PAGO AL REY
Este fin de semana os voy a proponer una de las versiones de dos acertijos clásicos (este primero más fácil) del mismo tipo. Espero que os guste.
El rey de un país oriental tiene un gobernador en cada una de sus provincias que anualmente llevan su tributo, consiste en un saco con un número indeterminado de monedas de oro de p gramos. Uno de los gobernadores hace trampa: todas sus monedas pesan un gramo de menos sin variar forma y tamaño (tienen una burbuja de aire en su interior). Con una balanza de dos platillos y un juego de pesas apto para pesar cualquier cantidad el rey tiene que averiguar en ¡una única pesada! cual es el gobernador que pretende engañarle. No es necesario saber cuántos gobernadores hay ni cuál es el tributo que paga cada uno.
La solución está tras el enlace.
viernes, 16 de septiembre de 2016
ACERTIJO 46 - NÚMEROS QUE SE SUMAN
Cada cifra, empezando por la tercera, de la representación decimal de un número de seis cifras es igual a la suma de las dos cifras anteriores. ¿Cuántos números de seis cifras tienen esta propiedad?
La solución se muestra tras el enlace.
La solución se muestra tras el enlace.
jueves, 15 de septiembre de 2016
ACERTIJO 45 - QUITANDO CARTAS
Hay 5 cajas con cartas nombradas A, E, I, O, U. Pedro quiere quitar cartas de las cajas de manera que al final quede una sola carta en cada caja, y cajas distintas contengan letras distintas. ¿Qué carta queda en la caja número 2?
La solución se muestra tras el enlace.
miércoles, 14 de septiembre de 2016
ACERTIJO 44 - ¡A CONTAR TRIÁNGULOS!
¿Cuántos triángulos hay en la figura que se muestra a continuación?

La solución se muestra tras el enlace.
La solución se muestra tras el enlace.
martes, 13 de septiembre de 2016
ACERTIJO 43 - LOS DADOS Y SU SUMA
Siete dados iguales se pegan juntos para formar el sólido de la figura: Las caras de los
dados que se pegan juntas tienen el mismo número de puntos en ellas.
¿Cuántos puntos hay, en total, en la superficie del sólido?
La solución se muestra tras el enlace.
lunes, 12 de septiembre de 2016
ACERTIJO 42 - ÁREAS SOMBREADAS
Dentro de un cuadrado de área 36 hay regiones sombreadas como se muestra en la figura
de la derecha. El área total sombreada es 27.
¿Cuánto vale a + b + c + d?
La solución se muestra tras el enlace.
domingo, 11 de septiembre de 2016
ACERTIJO 41 - SUMA DE RAÍCES
La suma de las raíces del conjunto de ecuaciones dado por la igualdad
es:
La solución se muestra tras el enlace.
es:
La solución se muestra tras el enlace.
sábado, 10 de septiembre de 2016
ACERTIJO 40 - LOS VECINOS DEL 8
Colocamos las cifras 1, 2, …, 9 en las casillas de un tablero 3x3, de modo que cada
casilla contiene una única cifra. Hemos colocado ya, como se muestra en la figura,
las cifras 1, 2, 3 y 4.
Se considera vecinos a dos números cuando sus casillas comparten un lado.
Después de colocar todas las cifras observamos que la suma de los vecinos de 9 es
15. ¿Cuánto vale la suma de los vecinos de 8?
La solución se muestra más abajo.
SOLUCIÓN: 27
viernes, 9 de septiembre de 2016
ACERTIJO 39 - NECESITO USAR EL BAÑO
Seis amigos comparten un piso con dos cuartos de baño, que utilizan cada mañana empezando a las 7h en
punto. Nunca hay más de una persona utilizando cada cuarto de baño. Tardan 8, 10, 12, 17, 21 y 22
minutos, respectivamente, en utilizar el cuarto de baño. ¿Cuál es la hora más temprana a la que pueden
terminar de usarlos?
La solución se muestra más abajo.
SOLUCIÓN: 7:46
La solución se muestra más abajo.
SOLUCIÓN: 7:46
jueves, 8 de septiembre de 2016
ACERTIJO 38 - LA RANA SALTARINA
En un estanque hay 16 hojas de nenúfares formando un cuadrado 4x4 como
se muestra en la figura, con una rana sentada en una de las esquinas. La
rana salta de una hoja a otra, horizontal o verticalmente. Siempre salta por lo
menos sobre una hoja y nunca aterriza en la misma hoja dos veces. ¿Cuál es
el mayor número de hojas (incluyendo la inicial) que puede alcanzar la rana?
La solución se muestra más abajo.
SOLUCIÓN: 16
miércoles, 7 de septiembre de 2016
ACERTIJO 37 - DIVIDE
Querría dedicar el acertijo de hoy a Kevin Maginsky amigo de aventuras matemáticas en Rusia y una bellísima persona fallecida recientemente.
Aquí va el acertijo del 7 de septiembre de 2016.
El número 1/1024000 se escribe en forma decimal, con el menor número posible de cifras. ¿Cuántas cifras aparecen detrás de la coma?
Aquí va el acertijo del 7 de septiembre de 2016.
El número 1/1024000 se escribe en forma decimal, con el menor número posible de cifras. ¿Cuántas cifras aparecen detrás de la coma?
La solución se encuentra más abajo.
SOLUCIÓN: 13
martes, 6 de septiembre de 2016
ACERTIJO 36 - CAZANDO RATONES
Cuatro gatos, Bill, Tom, Minnie y Liz fueron a cazar ratones. Tom y Liz juntos cazaron tantos ratones como Minnie y Bill. Bill cazó más ratones que Minnie. Bill y Liz juntos cazaron menos ratones que Tom y Minnie juntos. ¿ Cuántos ratones cazó Minnie , si Tom cazó 3?
La solución se muestra más abajo.
SOLUCIÓN: 1
lunes, 5 de septiembre de 2016
ACERTIJO 35 - MÉTODOS DE ESTUDIO
Juana tiene que resolver 40 preguntas. Su madre le ofrece 1/2 Euro por cada pregunta que contesta correctamente, pero Juana debe pagar 1 Euro por cada contestación incorrecta. Después de contestar a todas las preguntas, Juana recibe 2 Euros de su madre. ¿ Cuántas preguntas contestó correctamente?
La solución se muestra más abajo.
SOLUCIÓN: 28
La solución se muestra más abajo.
SOLUCIÓN: 28
domingo, 4 de septiembre de 2016
ACERTIJO 34 - APOSTANDO AL JUEGO
Alberto, Benito y Carlos ponen dinero en un juego en la proporción 1:2:3.Después del juego, se reparten el dinero que han puesto en la proporción 4:5:6. ¿ Qué sucedió?, ¿ganaron o perdieron dinero?, ¿ o nada de eso?
La solución se muestra más abajo.
SOLUCIÓN: Alberto ganó, Carlos perdió y Benito no ganó ni perdió.
La solución se muestra más abajo.
SOLUCIÓN: Alberto ganó, Carlos perdió y Benito no ganó ni perdió.
sábado, 3 de septiembre de 2016
ACERTIJO 33 - COLOCA A LOS CUADRADOS
Jimmy tiene 9 cuadrados del mismo tamaño. Tres de ellos son blancos, tres son azules y tres son rojos.
¿ De cuántas maneras distintas se pueden disponer en una tabla 3x3 de modo que cada fila y cada columna contengan cuadrados de los tres colores?
¿ De cuántas maneras distintas se pueden disponer en una tabla 3x3 de modo que cada fila y cada columna contengan cuadrados de los tres colores?
La solución se muestra más abajo.
SOLUCIÓN: 12
viernes, 2 de septiembre de 2016
ACERTIJO 32 - UNO DE CEROS
¿En cuántos ceros termina el producto 201325x201326x201317?
La solución se muestra más abajo.
SOLUCIÓN: 1
La solución se muestra más abajo.
SOLUCIÓN: 1
jueves, 1 de septiembre de 2016
ACERTIJO 31 - ALICIA Y LA LIEBRE
La Liebre de Marzo siempre miente de Lunes a Miércoles. Dice la verdad los demás días de la semana. Un día se encuentra a Alicia y dice:
i) ''Ayer mentí''
ii) ''Pasado mañana mentiré durante dos días seguidos''
i) ''Ayer mentí''
ii) ''Pasado mañana mentiré durante dos días seguidos''
¿Qué día vio Alicia a la liebre?
La solución se muestra más abajo.
SOLUCIÓN: El Lunes.
miércoles, 31 de agosto de 2016
ACERTIJO 0 - SUMANDO PARA EMPEZAR
Como ya hicimos el año pasado vamos a proponer durante todo el mes de septiembre todos los días a las 10 tendréis un acertijo (advierto que son algo más difíciles que el año pasado, pero no mucho) intentando buscar incrementar un poco la dificultad cada día y acabando como en 2015 con un acertijo dificultad extrema. Aquí os dejo con uno para abrir el apetito, mañana comenzamos por el acertijo 31 (donde lo dejamos el año pasado).
6+4=210
8+3=511
8+7=115
11+7=418
15+3=?
La solución como siempre, se muestra más abajo.
SOLUCIÓN: 15+3 = 1218; (15-3)_(15+3) = (12)_(18) = 1218
viernes, 19 de agosto de 2016
1989
19 del 8 a las 9 = 1989, ¿qué propiedad especial esconde este número? Os dejo unos días para pensarlo, comentad vuestras ideas y en unos días os lo contaré. Es algo realmente interesante.
sábado, 13 de agosto de 2016
LAS MATEMÁTICAS DE LA MADRE RUSIA
Como prometí, voy a contaros mis andanzas por la madre Rusia, pero voy a limitarme a las aventuras matemáticas, porque como comprenderéis, si os contará todas las anécdotas del grupo de españoles que veis aquí abajo, tendría para mucho pero que mucho tiempo...
 |
| Grupo de españoles "rusos" |
Partimos de España el 30 de junio y tras un par de aviones, tres o cuatro cacheos en el aeropuerto de San Petersburgo y un taxista un poco desorientado llegamos al lugar del campamento, un lugar realmente idílico y tranquilo perfecto para la práctica de las matemáticas, situado cerca de la localidad de Losevo, en un bosque junto a un largo de un tamaño bastante amplio.
La verdad es que un lugar precioso para pasar ir a relajarte. Pero pasando ya a las matemáticas... se nota porque los rusos nos sacan tanta ventaja en lo que al arte matemático concierne, allí hay tradición matemática, existen multitud de Olimpiadas de distintos tipos y dificultades, tienen lo que ellos denominan círculos matemáticos (una especie de seminarios), en el instituto no se limitan a dar nuestras mecánicas e inservibles matemáticas de ESO que solo sirven para cortar de golpe con la capacidad de abstracción, el ejemplo más claro de esto último es la geometría, mientras que nosotros apenas la tocamos y cuando lo hacemos limitamos el pensamiento para aprender a manejar la geometría analítica ellos pueden elegir en clase una asignatura dedicada solo a las matemáticas. Pero bueno, como no creo que nuestro sistema educativo cambie (para bien quiero decir, porque cambiar lo hará, que hay que inventarse leyes absurdas) da igual.
En nuestro primer día nos enfrentamos a nuestra primera Olimpiada, con una duración de unas 3 horas era una Olimpiada con un formato algo distinto a las que los españoles estamos acostumbrados. Empezábamos con 5 problemas, en cuanto resolvías uno, o creías haberlo hecho, ibas a explicárselo de forma oral a uno de los profesores, podías tenerlo bien y pasar a otro o los correctores podían considerar que estaba incompleto o mal, tenías tres intentos para cada problema. Así, cuando resolvías 3 de los 5 te daban otros 2 problemas. El objetivo, claramente, era resolver el mayor número de problemas posibles.
Tras ello, empezamos con las clases, geometría de masas la primera semana (muy interesante por cierto) y teoría de conjuntos la segunda con alguna conferencia entre medias y con trubogranniks en el tiempo libre. Pero, en mi opinión el mejor día de todos fue el de la BATALLA MATEMÁTICA, cerca de 10 frenéticas e intensas horas casi seguidas de matemáticas, un gran descubrimiento. empezamos con dos equipos de seis cada uno y 10 problemas para intentar resolverlos entre los seis en un plazo de 5 horas, tras ello comida, pensar estrategias y, ¡dispuestos a comenzar con lo bueno! Explicaré las reglas, tenemos dos equipos como ya sabéis que han estado un determinado tiempo resolviendo los mismos 10 problemas, tras un determinado proceso elegimos que equipo comienza (normalmente un problema de agilidad mental). Aquel que tiene el derecho a empezar reta al otro a un problema, este equipo acepta el reto o lo rebota, en ambos casos sale un representante de cada equipo (cada persona puede salir un máximo de dos veces), si el equipo ha aceptado el reto es su representante quien lo resuelve y si no el otro. Una vez se acaba la explicación, su rival intenta desmontar la solución propuesta por todos los medios (lo que viene a ser tocar las narices todo lo que pueda) hasta que diga que está conforme con la solución (los equipos pueden pedir hasta 6 tiempos muertos para apoyar a sus compañeros durante 30 segundos por cada tiempo muerto). Una vez el rival ha acabado con su fase de "tocar las narices" empieza a hacerlo el jurado y cuando acaba reparte 12 puntos entre el jurado y ambos equipos (también cabe destacar que si un reto ha sido rebotado y no ha sido resuelto correctamente el equipo que retó deberá hacerlo de nuevo). Mientras que las batallas de nuestros compañeros duraron en torno a las 2 horas la nuestra, tremendamente igualada necesitó de 5 horas para decidir el vencedor pese a que ambos equipos pedían ya un empate amistoso, pero mereció la pena, sobre todo porque a mí en particular me tocó desmontar una solución de un problema que mi rival se iba inventando sobre la marcha y que parecía estar bastante atinada, buena y rápida imaginación, eso desde luego.
Al acabar el campamento muchas lágrimas los diplomas correspondientes y una semanita de vacaciones en San Peters burgo pero con nuevos conocimientos, nuevas amistades y sobre todo muchos recuerdos bonitos.
LOS "MATERRUSOS":
lunes, 8 de agosto de 2016
EL PROBLEMA DEL CABALLO
Un día navegando por ahí me topé con este vídeo sobre el salto del caballo y muchas cosas más... Espero que lo disfrutéis y que os guste tanto como yo:
lunes, 25 de julio de 2016
BECAS EUROPA XII ALEJANDRO FERNANDEZ JIMENEZ
Este es el vídeo que voy a presentar al concurso "Becas Europa XII", vídeo en el cual tenías el siguiente tema "¿Qué te gustaría no olvidar dentro de 20 años? Envía un vídeo a tu yo del futuro..." y he aprovechado para poner algunas cosillas de mates y así presentároslas por encima entre las que destaco la regla de cálculo y los trubogranniks, un descubrimiento que he hecho en Rusia (en el vídeo estoy construyendo un icosaedro truncado a la tercera parte o "balón de fútbol" para los amigos) así que prometo colgar en un futuro no muy lejano entradas que expliquen estas dos novedades. Espero que os guste el vídeo.
martes, 28 de junio de 2016
LII OLIMPIADA MATEMATICA ESPAÑOLA BARCELONA, MI VISIÓN DEL "CONCURSANTE"
Como prometí voy a escribir una entrada de las Olimpiadas desde el punto de vista de uno de los participantes (de los normalillos) que tuvimos la suerte de competirla. Espero que os guste.
Este año tocaba celebrar las Olimpiadas en Barcelona (a la vez que el Barça-Madrid), en la Politécnica y la verdad, es que se esmeraron en evitar que tuviéramos un segundo libre. Nada más llegar a Barcelona (con algún contratiempo que me impidieron llegar con mi profesor responsable y el medalla de oro del año pasado) nos equiparon con nuestras acreditaciones naranjas necesarias para hacer el examen, nos indicaron cual sería nuestra habitación las próximas tres noches y nos hicieron la foto correspondiente.
 |
| Equipo Castilla y León |
Una cena tranquila para conocer un poco al resto de participantes y directos a la cama para dormir (aunque poco debido al extremo calor y sobre todo a los nervios) y a la mañana siguiente ya nos estábamos dirigiendo a realizar la primera parte del examen, ya sabéis tres horitas y media para tres problemas cuyos enunciados apenas superan las tres o cuatro líneas. Además de ser un examen duro, también fue uno de los más protocolarios que he vivido. Primero, nos nombraban por orden alfabético y tras enseñar nuestra acreditación esperábamos turno para hacernos una foto individual (aunque no se que ha sido de ellas) y nos dirigíamos a la sala del examen a buscar nuestro DNI y nuestro número asignado (el mío el 24) para encontrarnos con tres carpetas (una para guardar cada problema), una bolsa con nuestro DNI para guardar relojes, móviles y demás cacibaches y una botellita de agua y papeles para responder y mandar nuestras dudas, por escrito, al tribunal durante la primera media hora. Y, lo que más me sorprendió, ¡al fondo del aula había cinco mesas repletas de dulces y bebidas para reponer fuerzas cuando quisiéramos! (aunque confieso que apenas los probé, falta de tiempo). Tras todo esto, nos desearon toda la suerte del mundo, nos dejaron unos papeles del ministerio que firmar para un hipotético premio y, a las 10 exactas comenzamos con la primera parte de la LII OME (al final de la entrada colgaré los problemas con sus soluciones).
He de confesar que no fue el examen de mi vida, apenas resolví la primera parte del tres (para luego después del examen descubrir que me había equivocado con un fallo bastante importante), el segundo lo intenté sin obtener resultados decentes y el primero sí que lo conseguí, más o menos como todos los allí presentes. De hecho, recuerdo, que la gran mayoría estábamos hechos polvo y realmente afligidos por haber sido superados, quizá demasiado, por el examen y llenos de un sentimiento de impotencia y al menos en mi caso cierta sensación de incompetencia que se reflejaba claramente en nuestras caras y en el ambiente. La lucha por los oros y por los bronces ya estaba bastante diferenciada tras el primer día.
Por la tarde nos llevaron al MMACA ("Museu de Matemàtiques de Catalunya") donde realizamos muchas actividades interactivas muy curiosas y tras ello se nos entregaron los diplomas por haber sido capaces de llegar hasta allí (aquí algunas fotos del museo).
Tras todo esto (y sus correspondientes partiditas de cartas con mis compañeros de habitación, los dos leoneses y unos catalanes muy majos) nos dispusimos a dormir para prepararnos para el segundo día de examen.
El sábado empezábamos a las 9:30, mismo protocolo (pero sin las fotos y con algunos llegando excesivamente justos de tiempo) y otros tres problemas con los que pegarnos durante tres horas y media. Yo había conseguido olvidarme del disgusto del día anterior y conseguí resolver el problema número cuatro (o al menos eso es lo que yo pienso y soy feliz haciéndolo), con el cinco no tuve mucho éxito y por último, con el sexto, pensé que había conseguido resolverlo, pero como muchos otros había caído en una trampa que había sido perfectamente tejida por y para nosotros y que solo uno los 77 allí presentes, el tercer clasificado en el computo global, fue capaz de resolver.
Por la tarde, una visita guiada para hacer tiempo para la corrección de exámenes y por fin, a las 19:30, el gran momento, la ceremonia de premios. Primero la presentación de autoridades, Xavier Jarqué (representando a la Asociación de profesores de matemáticas de Cataluña), Francisco Marcellán (presidente de la RSME), Miquel A. Essomba (representando al Ayuntamiento, o más bien dejándolo en ridículo, llegó bastante tarde y encima empezó hablando en catalán por error), Meritxel Ruiz (la Consejera),Violeta de Miguel (representando al Ministerio) y el rector de la Politécnica. El acto no tuvo desperdicio, en cuanto Marcellán tuvo la palabra, no paró de atacar al Ministerio lanzando verdades como puñales sobre las pésimas e inaceptables condiciones y tratos que se les da a la enseñanza y a la investigación en este país a lo que la representante del Ministerio trato de defenderse con poco éxito y bastante aturdida y descolocada.
 |
| Mesa de autoridades |
Y tras todo el acto, prosiguió el nombrado de todas y cada una de las treinta y seis medallas (dieciocho de bronce, doce de plata y seis de oro) empezando por la última. Y comenzando por la medalla treinta y seis anunciaron: "décimo octava medalla de bronce, va para Castilla y León", los tres castellano y leoneses que estábamos juntos nos miramos con sorpresa y tras ello nombran "Alejandro Fernández Jiménez". No sé que pensarían los otros treinta y cinco que recibieron su medalla pero yo (además de chupar mucha cámara por ser el primero en subir al escenario) sentí una mezcla de emociones entre sorpresa (no me la esperaba), alegría y agradecimiento por darme el bronce treinta y seis (que suele ser una lotería en la que muchos no consiguen medalla). Castilla y León se llevó también la primera medalla de plata gracias a Aitor (a una del oro y de representar a España en las Internacionales, aunque estaba contento porque tampoco se la esperaba) y Don Marcos García Fierro, esta vez no pudo ser, Marcos ganó un oro y un bronce internacional cuando estaba en tercero de la ESO, sin embargo, "el excelente impulso" y "la grandiosa ayuda" que se da en este país a los que se dedican a pensar (no como a los que solo dan patadas a un balón) ha hecho que, en mi opinión, este país haya perdido una buenísima oportunidad de ganar su primera medalla de oro en unas Internacionales (pero bueno, ya sabemos como es España). Tras esto nos fuimos de cena y al día siguiente la delegación de Valladolid nos dedicamos a hacer algo de turismo. Aquí os dejo fotos de los medallistas y el listado de los treinta y seis alumnos pre-universitarios que mejor hemos combinado la suerte y la habilidad matemática este año.
 |
| Yo recogiendo mi medalla 31-36 |
 |
| 25-30 |
 |
| 19-24 |
 |
| 16-18 |
 |
| 13-15 |
 |
| 10-12 |
 |
| 9 |
 |
| 8 |
 |
| Aitor 7 |
 |
| 6 |
 |
| 5 |
 |
| 4 |
 |
| 3 |
 |
| 2 |
 |
| 1 |
 |
| Equipo Olímpico Español 2016 |
 |
| Medallas Castilla y León |
 |
| Listado oros y platas |
 |
| Listado bronces |
Aquí os dejo un enlace a la página oficial de la LII OME:
Y un segundo enlace a los problemas resueltos:
Suscribirse a:
Entradas (Atom)