ONDÍCULAS

"Yves Meyer (francés), Ingrid Daubechies (belga y estadounidense), Terence Tao (australiano y estadounidense) y Emmanuel Candès (francés) han realizado contribuciones pioneras y trascendentales a las teorías y técnicas modernas del procesamiento matemático de datos y señales. Estas son base y soporte de la era digital -al permitir comprimir archivos sin apenas pérdida de resolución-, de la imagen y el diagnóstico médicos -al permitir reconstruir imágenes precisas a partir de un reducido número de datos- y de la ingeniería y la investigación científica -al eliminar interferencias y ruido de fondo-.''

Así reza el comunicado de la Fundación Princesa de Asturias por el cuál se concedió el Premio Princesa de Asturias de Investigación Científica y Técnica 2020 a los matemáticos Yves Meyer (doctor honoris causa por la UAM), Ingrid Daubechies, Terence Tao y Emmanuel Candès. Todo un hito para esta disciplina.

Fotografía los premiados tomada de la Fundación Princesa de Asturias. De izquierda a derecha, Meyer, Daubechies, Tao y Candès.

Pero, ¿qué hicieron exactamente? Bien, la respuesta tiene que ver con algo conocido como teoría de ondículas, muy importantes porque consiguen dividir imágenes y sonidos en obetos matemáticos más pequeños y manejables pero manteniendo los detalles en gran detalle, eliminando ruidos e interferencias, comprimiendo sin apenas pérdida de calidad.

Los pioneros fueron Meyer y Daubechies (las ondículas ya le sirvieron a Meyer en 2017 para ganar el Premio Abel), y más adelante Tao y Candès completaron su trabajo con estudios relacionados con la teoría del compressed sensing, que permite la reconstrucción eficiente de datos dispersos basados en muy pocas mediciones. Las aplicaciones son muchas y de gran relevancia para nuestra vida cotidiana, como por ejemplo procesamiento de imágenes, reconocimiento de voz, múltiples campos de la medicina, geofísica o astrofísica entre otros. Por todo esto, queremos que este breve artículo te introduzca a una de las ramas de las matemáticas de mayor actualidad.

El descubrimiento.

La historia del origen de estos artefactos matemáticos es cuanto menos curiosa. Yves Meyer estaba esperando a que uno de sus colegas de la École Polytechnique terminara de fotocopiar un artículo de Jean Morlet y Alex Grossmann (de Marsella) sobre una nueva técnica para descomponer las señales sísmicas complejas registradas en los terremtos. Meyer cogió una copia de este artículo y se percató de que contenía elementos similares a teorías de descomposición de funciones de Análisis Armónico (su rama de especialización en ese momento). Ese mismo día, tomó el tren a Marsella para conocer a los autores y a partir de ahí el resto es historia, las ondículas, resultado final de esta intrigante anécdota, se convirtieron en una teoría que ha inspirado muchos trabajos de matemáticos, físicos e ingenieros durante los últimos años.

Acto de investidura de Yves Meyer como Doctor Honoris Causa en la Universidad Autónoma de Madrid, el 6 de junio del año 1997. De izquierda a derecha, Adolfo Quirós, Julián de la Horra, José García-Cuerva, Ireneo Peral, Alberto Pedro Calderón, Antonio Córdoba, Yves Meyer, Miguel de Guzmán y Santiago Carrillo. Fotografía cedida por el Departamento de Matemáticas de la UAM.

Bien, la historieta está muy chula y sirve para introducir el tema, pero, ¿no te estás preguntando qué son exactamente estos bichos? Sobre esto, seguro que has oído hablar en algún momento de las series de Fourier (y si no, no pasa nada porque te lo explicamos aquí). 

La idea principal detrás de las series de Fourier es aproximar funciones por medio de senos y cosenos. Es muy fácil, coge una función $f$ periódica con periodo $T$, esto quiere decir que $f(x) = f(x+T)$ para todo $x$ real, cualquiera nos sirve -en esencia, Fourier estudia funciones en un ``trozo'' de la recta real, para aplicar Fourier repites el ``trozo'' por toda la recta real y ya estaría-. 

Tomemos la serie $s_N$ formada por los elementos

$s_N (t) = \frac{a_0}{2} + \sum_{n=1}^N \left[ a_n \cos \left(\frac{2n \pi}{T}t \right) + b_n \sin \left( \frac{2n \pi}{T} t \right) \right]$,

con

$a_0 = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \, dt$, 

y

$a_n = \frac{2}{T} \int_{-T/2}^{T/2} f(t) \cos \left(\frac{2n \pi}{T}t \right) \, dt, $

$b_n = \frac{2}{T} \int_{-T/2}^{T/2} f(t)   \sin \left(\frac{2n \pi}{T}t \right) \, dt$,

llamados los coeficientes de Fourier. Si tomamos límite en $N$, se tiene que para casi todo punto, se satisface

$\lim_{N \to \infty} s_N(t) = f(t)$.

(Se necesitan algunas condiciones extra sobre $f$, $f \in L^2$, algo que escapa de las pretensiones de este texto pero, que no cunda el pánico, no es una condición muy exigente). Pero, claro, ahora seguramente te estarás preguntando (y con muy buen criterio, todo sea dicho): "Muy bien, pero, ¿y esto para qué?, si ya tengo una expresión de $f$ para qué quiero otra más complicada''.

$s_N$ converge a $f$ en casi todo punto, es decir, cuanto más grande sea $N$ (y más coeficientes de Fourier usemos), más se parecerá $s_N$ a $f$. Esto es importante sobre todo para almacenar funciones y trabajar con ellas computacionalmente de forma mucho más eficiente. En vez de tener que guardar el valor de la función en los puntos, basta con que guardemos un puñado de puntos para tener una muy buena aproximación de $f$ con la que poder trabajar, y por ende, consumimos mucha menos memoria del ordenador.

El problema es que el diablo vive en los pequeños detalles, y esta no es una excepción, por desgracia... Que $s_N$ converja a $f$ no nos dice nada sobre la velocidad de esta, puede que tengamos una aproximación decente de $f$ para $N=10$ o que tengamos que esperar hasta $N=1.000.000.000.000$, y claro, si tenemos que esperar hasta coeficientes tan altos, esta idea tan maravillosa de Fourier se vuelve incapaz de ayudarnos con el almacenaje de datos. 

En particular, las series de Fourier, son sumas de senos y cosenos, funciones "demasiado suaves'', es decir, muy redonditas y muy poco abruptas. Por esta suavidad "excesiva'', cuando las funciones tienen algún punto muy "picudo'', se necesitan demasiados pasos hasta que la serie de Fourier da aproximaciones decentes de $f$ (el ruido del que hablábamos al principio del texto, y que, desgraciadamente, las series de Fourier eliminan porque aproximan con senos y cosenos superpuestos).

La pregunta clave que surge ahora después de todos estos razonamientos es la siguiente, si cambiamos el tipo de curvas y en vez de usar senos y cosenos recurrimos a otras, ¿podríamos corregir este inconveniente?

Las ondículas pretenden dar la solución. En la década de los 80s Meyer construyó el primer ejemplo de ondículas no-triviales, continuamente diferenciables. Dos años después, Daubechies consiguió describir una familia de ondículas que formaban una base de funciones ortonormales con soporte compacto, o en cristiano, la matemática si no hizo magia, poco le quedó. Resultados muy elegantes, que constituyen el pilar de las ondículas hoy en día y que consiguen la solución al problema que planteábamos.

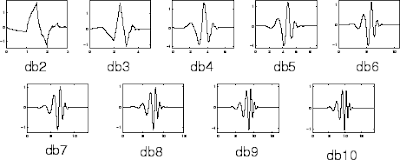Familia de ondículas Daubechies $dbn$.

Por ejemplo, usando las ondículas de Daubechies $dbn$, dilatándolas y trasladándolas apropiadamente para que estas formen una base, un tecnicismo necesario para poder abarcar todo el rango de funciones que necesitamos, estaríamos expresando nuestra función como una serie que depende de los elementos $dbn$ y no de los $\cos \left( \frac{2n \pi}{T} t \right) + \sin \left( \frac{2n \pi}{T} t \right)$ como lo hace en Fourier. Con las $dbn$ nos referimos a la familia de curvas que se puede ver en la Figura anterior.

Compressed sensing.

Al principio de este artículo decíamos que la teoría de ondículas permitía dividir imágenes y sonidos en objetos matemáticos más manejables. Esto se consigue gracias al compressed sensing, o muestreo comprimido, una de las aplicaciones más relevantes de las ondículas en nuestro día a día. 

Fruto de la colaboración entre Terence Tao y Emmanuel Candès (entre otros), durante la primera década del siglo XXI se produjo una revolución en las técnicas de tratamiento de datos y señales gracias al desarrollo del compressed sensing. Esta teoría es especialmente útil porque permite la reconstrucción eficiente de datos dispersos basados en muy pocas mediciones.

En este artículo queremos explicar cómo funciona esta técnica. Para poder centrarnos en la idea que hay detrás de ella y no perdernos en los tecnicismos, vamos a tomar el ejemplo más sencillo, el de la cámara.

El objetivo de una cámara es, por supuesto, hacer fotos. Ahora bien, es una práctica común que la cámara comprima la imagen. Por ejemplo, si el tamaño inicial de la fotografía es de $2$MB sería normal quedarse con algo que ocupe menos, por ejemplo $200$KB, que es un $10 \%$ del tamaño inicial. La cosa, o la clave detrás de esta idea es, que, mientras el espacio de todas las imágenes tiene un valor de $2$MB de "grados de libertad'', el espacio de todas las imágenes interesantes (las partes que contienen los detalles relevantes de la fotografía) es mucho más pequeño y puede almacenarse en un espacio mucho más pequeño si a uno no le importa perder un poco de calidad.

No hace falta decir que existen varias formas de comprimir imágenes. Para comenzar a calentar podemos presentar una primera un poco "ingenua''. Supongamos que en nuestra foto encontramos un cuadrado monocromático muy grande, por ejemplo de $ 100 \times 100$ píxeles, que son de exactamente el mismo color. Si no hiciéramos ninguna compresión, usando una escala de grises $8$-bit, almacenar toda la información de este cuadrado requerirían $10000$ bytes, cuando, lo único que necesitas es almacenar la dimensión, la localización y el color usados (que es mucha menos información). Por supuesto, esta idea no nos sirve en la práctica ya que, por ejemplo, no consigue dar resultados satisfactorios para las transiciones abruptas entre dos colores. 

Desde luego, este primer método queda lejos de ser ideal, en realidad, para resolver este problema se ha llegado al consenso en la comunidad científica de que resulta que es mejor no trabajar usando el color medio de cada cuadradito, sino que lo más óptimo es utilizar los desequilibrios medios. En otras palabras, cuan más intensa es de media la mitad derecha del cuadradito en comparación con la mitad izquierda del mismo cuadradito. Y, esto se puede formalizar utilizando sistemas de ondículas, que nos permiten expresar una imagen como la superposición lineal de varias ondículas. En la práctica, se utilizan técnicas más complejas, pero esto es suficiente para entender las ideas detrás del compressed sensing.

Visto esto, volvamos a nuestro ejemplo anterior, la imagen original tiene $2$ millones de grados de libertad, y, en particular si uno quiere expresar esta imagen en términos de ondículas, necesitaría $2$ millones de ondículas diferentes para poder reconstruirla perfectamente. No obstante, una imagen típica interesante es muy dispersa en una base de ondículas. Es muy posible que no necesitemos más de unas cien mil ondículas para poder capturar todas las características importantes de la imagen, y que el $1.9$ millón de ondículas restantes tan solo contribuyan a una pequeña cantidad de ruido aleatorio, invisible para la mayoría de los observadores.

Ahora, si nosotros (o la cámara) supieramos cuáles son los $100$ mil coeficientes de las ondículas que vamos a utilizar, entonces la cámara podría simplemente medir el valor de solo esos coeficientes y ni siquiera molestarse en intentar obtener el resto. (Es posible medir un único coeficiente aplicando un filtro adecuado a la imagen y haciendo una medida de una única intensidad del resultado obtenido.) No obstante, la cámara no conoce a priori cuáles son los coeficientes claves, así que tiene que obtener los $2$ millones de píxeles, convertir la imagen a una base de ondículas, localizar los $100$ mil coeficientes dominantes, almacenarlos y desechar el resto. Este es el problema en el que las mates obran un pequeño milagro.

Con esto en mente, la filosofía principal del compressed sensing es esta: Si uno necesita solo $100.000$ coeficientes para recuperar la mayor parte de la imagen, ¿por qué no tomar solo $100.000$ medidas en lugar de $2$ millones? (En la práctica tomaremos un margen de seguridad tomando por ejemplo $300.000$ medidas.) Claro, existe una dificultad evidente, tal y como decíamos antes, la cámara no sabe de antemano que cien mil coeficientes de los dos millones de coeficientes de ondículas son los importantes que se necesitan guardar. De esta forma, una pregunta que resulta muy interesante es saber qué pasa si seleccionas un conjunto completamente diferente de $100.000$ (o $300.000$) ondículas, ¿se perdería toda la información interesante en la imagen?

La solución a esta pregunta son las dos cosas, simples y poco intuitivas. Esta es hacer $300.000$ medidas que no tengan nada que ver con la base de ondículas. La idea es generar medidas (pseudo-)aleatorias, generando al azar $300.000$ imágenes -"máscaras''- y midiendo hasta qué punto se parece la imagen con la que estamos trabajando a las máscaras. Ahora, estas medidas (o "correlaciones'') entre la imagen y las máscaras serán, con casi toda seguridad, muy pequeñas, y muy aleatorias. Pero, y esto es el punto clave, cada una de las $2$ millones de ondículas que comprimen la imagen generará su propia "firma'' distintiva dentro de estas medidas aleatorias, y, por tanto, (con una probabilidad desorbitadamente alta) cada una de las firmas será distinta. Además, resulta que la combinación lineal de hasta $100$ mil de estas firmas serán distintas (se puede entender desde una perspectiva del álgebra lineal, esto significa que dos subespacios de dimensión $100.000$ de un espacio de dimensión $300.000$ elegidos de forma aleatoria, serán casi siempre disjuntos). Por esto, en principio es posible recuperar la imagen (o al menos sus $100.000$ componentes más importantes) a partir de estas $300.000$ medidas aleatorias.

En esencia, entender una imagen de $2$ millones de píxeles en una base de ondículas nos garantiza que eligiendo solo $300.000$ de estas de forma completamente aleatoria, $100.000$ de ellas nos permitirán recuperar la imagen con mucha precisión.

Para recuperar la imagen evitando ruidos habrá que usar algunas técnicas de recuperación de algoritmos no triviales. Pero, eso ya es tela de otro costar, y quizás... Para otro día.

Por último, puede ser interesante repasar algunas de las aplicaciones de esta idea tan abstracta del compressed sensing (siempre es bonito cuando ves las matemáticas de la carrera aplicadas a nuestro día a día):

• Imagen por resonancia magnética: En medicina, una resonancia intenta recuperar una imagen (la densidad del agua en el cuerpo humano) a partir de un número grande, pero finito, de medidas. Por el número de medidas necesitadas, el proceso es lento para el paciente, y las técnicas de compressed sensing pueden reducir el número de medidas necesitadas significativamente, llevándonos a procesos más rápidos.
• Astronomía: Muchos fenómenos astronómicos (por ejemplo los púlsar) tienen varias frecuencias de oscilación que los puede provocar que se dispersen o compriman mucho en distintos dominios de frecuencia. En este caso las técnicas de compressed sensing permiten medir estos fenómenos en el dominio temporal (a partir de datos del telescopio) consiguiendo reconstruir la señal original con precisión incluso a partir de datos incompletos o ruido.
•  Códigos lineales: En este caso el compressed sensing nos proporciona una método simple para combinar el output de varios transmisores de tal forma que si una fracción importante del output se pierde o se daña, todavía podamos recuperar la transmisión original.

Esta entrada es un artículo que escribí como parte del primer número de la revista QED, una iniciativa de alumnos y ex-alumnos en matemáticas de la Universidad Autónoma de Madrid. Lo mejor de todo es que esta es gratuita y de acceso libre para todo el mundo aquí. Así que si te ha gustado no lo dudes más y ve a leer el resto de la revista. ¡Seguro que te encantará!

Este post forma parte del Carnaval de Matemáticas, que en esta nonagésima octava edición, también denominada 13.1, está organizado por Rafael Martínez González a través de su blog El mundo de Rafalillo.